Best strategy for a fencing relay
The riddle
You are the coach at Riddler Fencing Academy, where your three students are squaring off against a neighboring squad. Each of your students has a different probability of winning any given point in a match. The strongest fencer has a 75 percent chance of winning each point. The weakest has only a 25 percent chance of winning each point. The remaining fencer has a 50 percent probability of winning each point.
The match will be a relay. First, one of your students will face off against an opponent. As soon as one of them reaches a score of 15, they are both swapped out. Then, a different student of yours faces a different opponent, continuing from wherever the score left off. When one team reaches 30 (not necessarily from the same team that first reached 15), both fencers are swapped out. The remaining two fencers continue the relay until one team reaches 45 points.
As the coach, you can choose the order in which your three students occupy the three positions in the relay: going first, second or third. How will you order them? And then what will be your team’s chances of winning the relay?
Functions and background
We need a function that simulates a relay:
simulateRelay = function(pOrder){
if(length(pOrder)!=3){
stop("The number of participants is 3.")
}
## Initialize
matchResult = NULL
myWins = 0
oppWins = 0
# First leg:
while(max(myWins,oppWins)<15){
if(runif(1) < pOrder[1]){
matchResult = c(matchResult,'myTeam')
myWins = myWins + 1
}else{
matchResult = c(matchResult,'opp')
oppWins = oppWins + 1
}
}
# Second leg:
while(max(myWins,oppWins)<30){
if(runif(1) < pOrder[2]){
matchResult = c(matchResult,'myTeam')
myWins = myWins + 1
}else{
matchResult = c(matchResult,'opp')
oppWins = oppWins + 1
}
}
# Final leg:
while(max(myWins,oppWins)<45){
if(runif(1) < pOrder[3]){
matchResult = c(matchResult,'myTeam')
myWins = myWins + 1
}else{
matchResult = c(matchResult,'opp')
oppWins = oppWins + 1
}
}
relayResult = ifelse(myWins==45,'My Team','The Opponent')
res = list('rres'=relayResult,'myWins'=myWins,'oppWins'=oppWins,
'allMatches'=matchResult)
return(res)
}Results
Before I present results, I’d like to state my idea of how this should work. My general thought is that the strongest player should go last. In general, I want my strongest player out for the longest time. If the order is from weakest to strongest, on average, we expect the following results:
- Weakest player will win 25% of matches, opponent wins 75% of the matches. So this player will be out for 20 matches, and get 5 wins. Score 5-15.
- Medium player will win 50% of matches, and should be out there for 30 matches total. Score 20-30.
- Best player will win 75% of matches and needs to win 25 matches before other player wins 15. Given the win probability, this player would be expected to win 25 matches in 33 tries.
If I play my best player in any spot but the last one, the most matches that can be won are 15, and my sense is that we want the player who can gain wins most efficiently out for the longest time.
playerProbs = c(0.25,0.5,0.75)
Nsims=10000
relayResTab = NULL
for(p1 in playerProbs){
otherProbs = playerProbs[playerProbs!=p1]
for(p2 in otherProbs){
p3 = otherProbs[otherProbs!=p2]
pOrder = c(p1,p2,p3)
relayWins = 0
for(n in 1:Nsims){
relaySim = simulateRelay(pOrder = pOrder)
relayWins = relayWins +
ifelse(relaySim$rres=="My Team", 1, 0)
}
winPct = relayWins/Nsims*100
orderTab = data.frame(p1,p2,p3,'WinPct'=winPct)
if(is.null(relayResTab)){
relayResTab = orderTab
}else{
relayResTab = rbind(relayResTab,orderTab)
}
}
}
## Order the table
relayResTab = relayResTab[order(-relayResTab$WinPct),]The labels in this table p1, p2, and p3 are the win probabilities of the first, second, and third players respectively.
| p1 | p2 | p3 | WinPct |
|---|---|---|---|
| 0.25 | 0.50 | 0.75 | 93.48 |
| 0.50 | 0.25 | 0.75 | 92.01 |
| 0.25 | 0.75 | 0.50 | 83.13 |
| 0.75 | 0.25 | 0.50 | 17.63 |
| 0.50 | 0.75 | 0.25 | 7.59 |
| 0.75 | 0.50 | 0.25 | 6.81 |
These results show that my intuition is correct, the strongest player going last is indeed optimal. In fact, any order that had the highest rated player after the lowest rated player made the team’s victory more than 80% probable.
Extensions
I thought it would be interesting to watch the win count change like a basketball game flow graph. This function will accomplish that goal.
plotMatchResult = function(matchResults){
numMatches = length(matchResults)
myRunWinTotal = c(0,cumsum(matchResults=="myTeam"))
myScore = data.frame('match'=0:numMatches,'team'='My Team',
'wins'=myRunWinTotal)
oppRunWinTotal = c(0,cumsum(matchResults=="opp"))
oppScore = data.frame('match'=0:numMatches,'team'='Opponent',
'wins'=oppRunWinTotal)
score = rbind(myScore,oppScore)
score$team = factor(score$team)
maxRunScore = pmax(myRunWinTotal,oppRunWinTotal)
matchNum = 0:numMatches
endFirst = matchNum[which(maxRunScore==15)[1]] + 0.5
endSecond = matchNum[which(maxRunScore==30)[1]] + 0.5
ggplot(data=score, aes(x=match, y=wins, group=team, color=team)) +
geom_step(aes(color=team), size=1.5) +
geom_hline(yintercept=15, linetype='dotted', color='red',size=1) +
geom_hline(yintercept=30, linetype='dotted', color='green',size=1) +
geom_vline(xintercept=endFirst, linetype='dotted', color='red',size=1) +
geom_vline(xintercept=endSecond, linetype='dotted', color='green',size=1) +
scale_color_brewer(palette='Dark2') +
theme_classic() + theme(text=element_text(size=24))
}
plotWinner = function(pOrder){
noWin = TRUE
while(noWin){
relayResult = simulateRelay(pOrder = pOrder)
noWin = relayResult$rres!="My Team"
i = 0
maxIter = 100
if(i>maxIter){
stop(paste('The simulation could not find a loss after',maxIter,
'iterations.'))
}
}
plotMatchResult(relayResult$allMatches)
}
plotLoser = function(pOrder){
noLoss = TRUE
maxIter = 100
i = 1
while(noLoss){
relayResult = simulateRelay(pOrder = pOrder)
noLoss = relayResult$rres!="The Opponent"
i = i+1
if(i>maxIter){
stop(paste('The simulation could not find a loss after',maxIter,
'iterations.'))
}
}
plotMatchResult(relayResult$allMatches)
}Optimal strategy
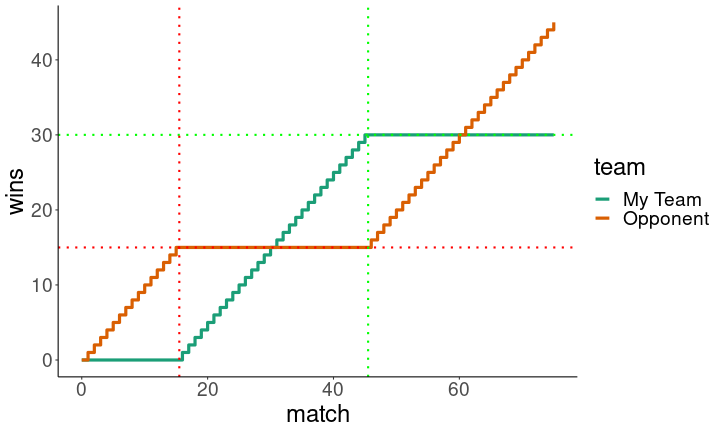
This strategy works in most cases. As I predicted, the opponent rushes out to a lead, but the top player makes up the difference in the end.
set.seed(1234)
plotWinner(c(0.25,0.5,0.75))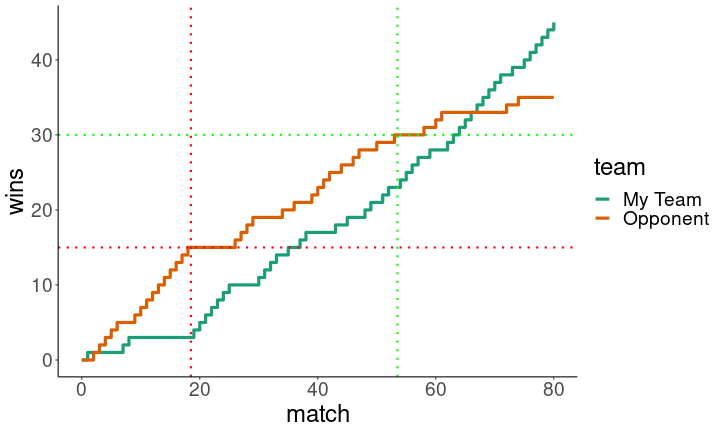
Obviously, this strategy isn’t foolproof. Sometimes, the opponent wins. When that happens, the lower ranked players don’t get as many wins as expected, and then the best player can’t quite make up the difference.
set.seed(1234)
plotLoser(c(0.25,0.5,0.75))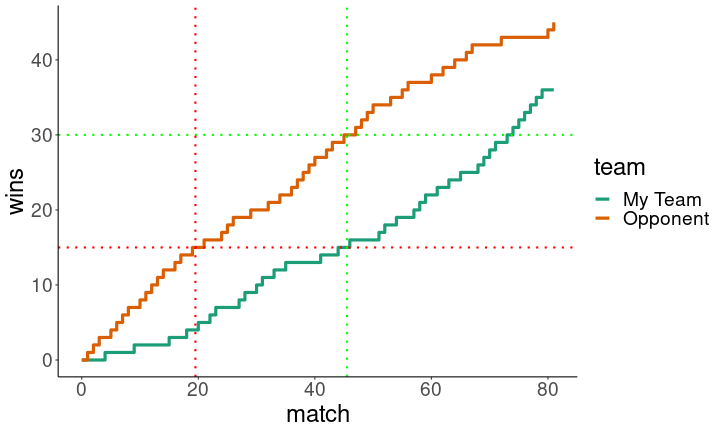
Worst strategy
And now let’s look at what happens when the coach strategically throws the match.
set.seed(12345)
plotLoser(c(0.75,0.5,0.25))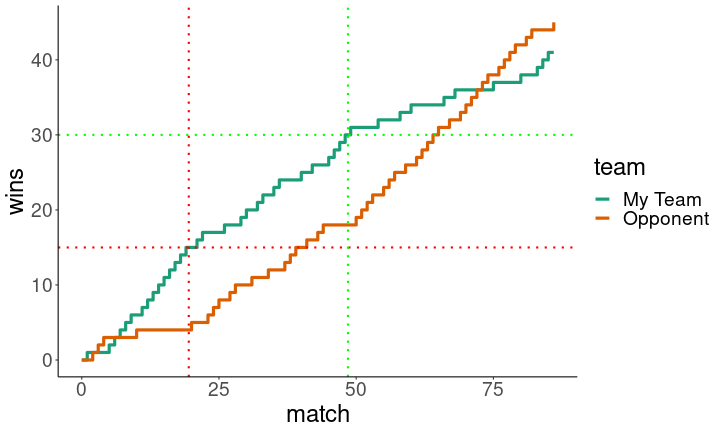
This case is the inverse of what happens when the team loses despite applying the optimal strategy. The team builds a big lead, and then is able to bring it home despite the weakest player’s struggles at the end.
set.seed(1234)
plotWinner(c(0.75,0.5,0.25))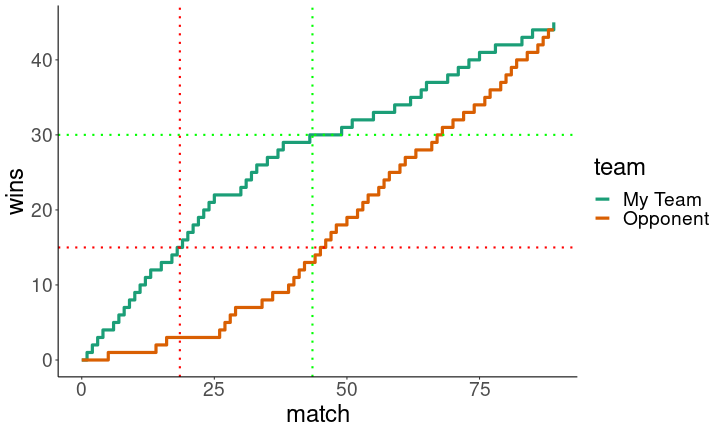
Rigging the game
Lastly, it occurs to me that if we came up with a rule like this:
You can distribute up to 1 point of win probability among your 3 players and deploy them as you see fit.
we can really rig the game. (I guess this team is “worse” than the team in question from an average match win probability perspective) In principle if you have players with win probabilities of 0, 0, and 1, you can always win the relay, or always lose the relay depending on your deployment. And the graphs look like this:
Always winning
45-30, every time.
plotWinner(c(0,0,1))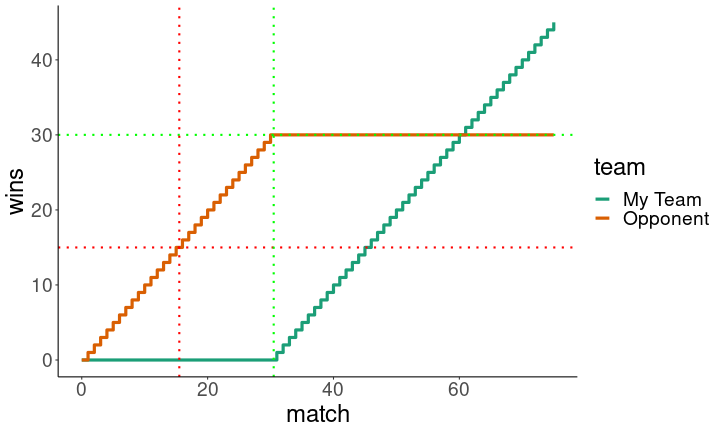
And never losing:
plotLoser(c(0,0,1))## Error in plotLoser(c(0, 0, 1)): The simulation could not find a loss after 100 iterations.Always losing
15-45, every time.
plotLoser(c(1,0,0))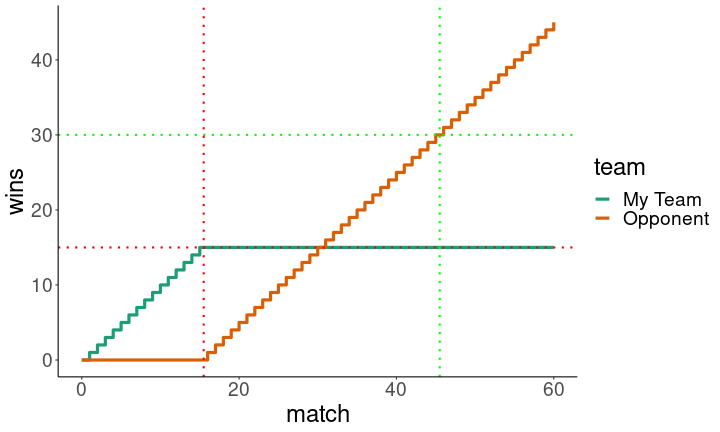
Or if you put your ringer second, it’s 30-45 every time.
plotLoser(c(0,1,0))