How Clever am I
The riddle
You are very clever when it comes to solving Riddler Express puzzles. You are so clever, in fact, that you are in the top 10 percent of solvers in Riddler Nation (which, as you know, has a very large population). You don’t know where in the top 10 percent you are — in fact, you realize that you are equally likely to be anywhere in the topmost decile. Also, no two people in Riddler Nation are equally clever.
One Friday morning, you walk into a room with nine members randomly selected from Riddler Nation. What is the probability that you are the cleverest solver in the room?
Results
Ok, so let’s start with some simple math. If I am cleverer than exactly 90% of people, which is my minimum cleverness percentile, if we pick one person from the general population, there is a 90% chance that I am cleverer than that person. If we pick 2 people, that would be \(0.9^2\) or a 81% chance that I am the cleverest. So for any number of people \(N\), I should be the cleverest with a probability of \(p=0.9^N\). For 9 people, that’s 38.7% of the time. This should be considered a lower bound on the correct answer.
Why is that a lower bound? Well, it’s because I know that I am at least in the 90th percentile of cleverness. There is some non-zero chance that I am cleverer than someone who is cleverer than 91% of people. Let’s see if we can figure this out by simulating this system. I’m going to write code which does this:
- Estimate my probability to be a random number between 0.9 and 1.
- Generate 9 random probabilities between 0 and 1 to simulate the room I’m walking into.
- Determine if my probability is larger than all of these and keep track of the result.
- Repeat a whole bunch of times and see where the probability stabilizes
simulateRoom = function(roomSize=9,myCleverBound=0.9){
myClever = runif(1,min=myCleverBound,max=1)
roomClever = runif(roomSize)
cleverest = ifelse(all(myClever>roomClever),1,0)
return(cleverest)
}
nSims = 10^5
roomResults = numeric(nSims)
for(i in 1:nSims){
set.seed(100*i)
roomResults[i] = simulateRoom()
}
cleverProb = cumsum(roomResults)/seq_along(roomResults)
cleverestProb = sum(roomResults)/nSims
plot(cleverProb,type='l',col='blue',ylim=c(0,1),xlab='simulation number',
ylab='cumulative probability', log='x')
abline(h=cleverestProb, col='red', lty=2)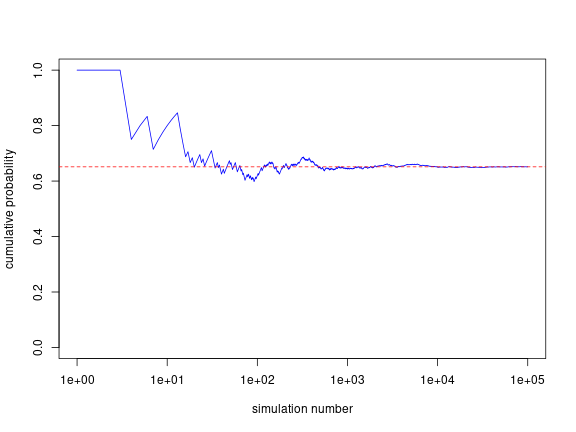
The value that this approaches is 65.1%.