Astronomical Enigma
The riddle
The astronomers of Planet Xiddler are back!
This time, they have identified three planets that circularly orbit a neighboring star. Planet A is three astronomical units away from its star and completes its orbit in three years. Planet B is four astronomical units away from the star and completes its orbit in four years. Finally, Planet C is five astronomical units away from the star and completes its orbit in five years.
They report their findings to Xiddler’s Grand Minister, along with the auspicious news that all three planets are currently lined up (i.e., they are collinear) with their star. However, the Grand Minister is far more interested in the three planets than the star and wants to know how long it will be until the planets are next aligned.
How many years will it be until the three planets are again collinear (not necessarily including the star)?
Functions and background
This is a simple least common multiple (LCM) type problem. I’m not going to write code to do this since the numbers are relatively easy, and I’m lazy. The way to find the LCM is to find the prime factorization of all of the numbers, and then determine the LCM by taking the unique prime factors and raising them to the largest power observed in each term, and then multiplying them together. For example, if we want to determine the LCM of 4 and 6, we need to find the prime factorization of each number:
- \[4 = 2^2\]
- \[6 = 2^1 3^1\]
The unique primes are 2 and 3. 2 is squared to get 4, and 3^1 is required to get 6. So the LCM is \(2^2 3^1 = 4\times 3 = 12\). Fourth grade math.
Results
So, our orbital periods are 3 years, 4 years, and 5 years. 3 and 5 are both prime numbers so the LCM is \(2^2 \times 3^1 \times 5^1 = 60\) years.
Extensions
Ok, so I’m totally a physics professor, and I can’t leave the blatant violation of Kepler’s 3rd law alone, textual footnote aside.
Kepler’s Third Law assumes that the force maintaining the orbit is a central force (that is, it depends only on the distance between two objects and acts on the line connecting those objects) AND that the force obeys the inverse-square relation, for gravity acting between point objects, this is:
\[F = \frac{GMm}{r^2} \propto \frac{1}{r^2}\]If we want to understand what is going on here, we need to relax the second assumption (inverse-square relation) and get a general statement of Kepler’s Third Law. If we assume that the central force is of the form of a power law:
\[F = \beta r^p\]Here, \(\beta\) is a numeric constant, \(r\) is the distance between the objects, and \(p\) is an unknown power. For circular motion, we can also write:
\[F = mr\omega^2 = \frac{4\pi^2 m}{T^2}r\]where \(m\) is the mass of the orbiting object and \(\omega = \frac{2\pi}{T}\) is the (constant) angular frequency of the rotation and \(T\) is the period of the motion. If we equate the two forces and solve for \(T\), we get:
\[T^2 = \frac{4\pi^2 m}{\beta} r^{1-p}\]Since we observe a pattern of \(T \propto r\), we know that \(1-p = 2\) implying that \(p=-1\). If we consider that the star could be a non-spherical shape, we can then determine that the observed power suggests that the star is in the shape of a very long, thin rod.
Alternative ideas
One thing that we can note is that Kepler’s laws only apply to the two-body problem, and there are many ways that having multiple celestial bodies can influence orbital mechanics. Precession, for example, is an orbit changing the direction in which it is distorted as depicted by the figure below. The article that I pulled this figure from specifically discusses this in the context of a test of general relativity, and is worth a read if you are interested.
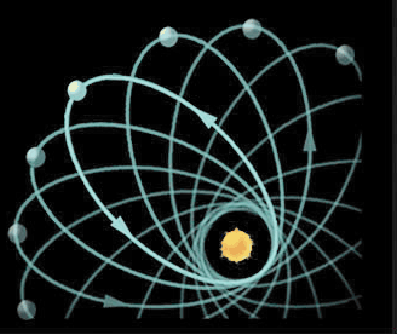
There is also the phenomenon of orbital resonance, whereby orbiting objects have orbital periods in a regular ratio with one another. These orbiting objects provide a regular gravitational “kick” which reinforces the resonance.
