Secret Santa

The riddle

Every year, CJ’s family of five (including CJ) does a book exchange for Christmas. First, each person puts their name in a hat. The hat is shaken, and then each person draws a random name from the hat and gifts that person a book. However, if anyone draws their own name, they all put their names back into the hat and start over.

What is the probability that no one will draw their own name?

Functions and background

I think brute force will work here. Let’s start by denoting each person in the family and generating all permutations of that group.

people = LETTERS[1:5]

perm = function(v){
    ## Let's generate all permutations recursively
    n = length(v)
    if (n==1){
        X = v
    }else{
        X = NULL
        for(i in 1:n){
            firstElement = v[i]
            remainingElements = v[-i]
            thesePerms = cbind(firstElement,perm(remainingElements))
            X = rbind(X,thesePerms)
        }
    }
    return(X)
}

allPerms = perm(people)

Results

Now, we just need to count all of the permutations which have at least one element in the same place as the original list of people.

isNoMatch = apply(allPerms,MARGIN = 1, FUN = function(x) !any(x==people))
prob = sum(isNoMatch)/length(isNoMatch)

The probability that nobody gets their own name is: 0.3667 or \(\frac{11}{30}\).

Extensions

So it would be nice to know how this probability changes as the number of players in the secret santa game changes. Let’s find out!

EDIT (12/11/2020):

Looking at the solution in next week’s riddler, I see that the probability of nobody getting themselves on a draw is:

\[P_N = \sum_{k=0}^N \frac{\left(-1\right)^k}{k!}\]

in the limit as \(N\rightarrow\infty\), we see that this simplifies to:

\[\lim_{N\rightarrow\infty} P_N = \frac{1}{e}\]

I will make this the value of the horizontal line on the plot below.

secretSantaMatch = function(N){
    if(N==1){
        ## If you are the only one in the secret santa, you always get your own name
        noMatchProb = 0
    }else{
        ppl = LETTERS[1:N]
        allPossibilities = perm(ppl)
        isNotMatch = apply(allPossibilities,MARGIN = 1, FUN = function(x) !any(x==ppl))
        noMatchProb = sum(isNotMatch)/length(isNotMatch)
    }
    return(noMatchProb)
}
n = c(1:10)
ssm = sapply(n,FUN=secretSantaMatch)
plot(n,ssm,xlab='number of people',ylab='probability for no matches',pch=20,col='blue')
abline(h=exp(-1),lty=2,col='lightblue')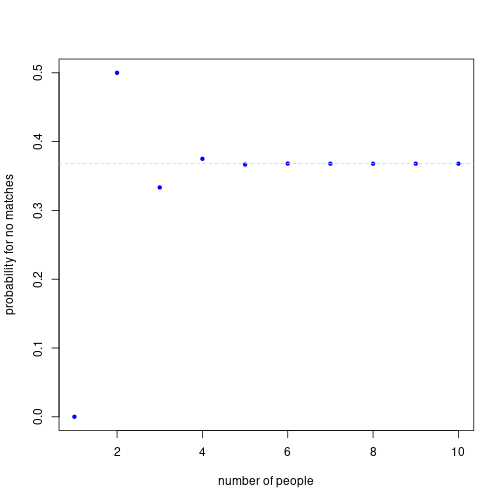

Given what we are observing here, it would seem that the need to re-draw occurs a little more than 1/3 of the time regardless of the size of the group. However, the number of permutations grows quickly \((N!)\), and I won’t be taxing my machine further. There is a steady (slow) growth in the curve, so I won’t rule anything out.

Extension #2: When does the game fail?

If we know the game will fail, which draw is the most likely culprit (we will stick to the \(N=5\) case for this)? First, let’s get only the permutations that fail.

## Only failed permutations
failPerms = allPerms[!isNoMatch, ]
## Figure out who drew his/her own name
drawFails = t(apply(failPerms, MARGIN = 1, FUN = function(x) x==people))
colnames(drawFails) = people
## Separate into single draw failures (only one name matched) and multi draw failures
singleFails = drawFails[rowSums(drawFails)==1, ]
multiFails = drawFails[rowSums(drawFails)>1, ]
## When a person draws their own name, they annonce it and quit, so subsequent drawings 
## don't matter/never happen
for(c in 1:ncol(multiFails)){
    multiFails[multiFails[ ,c], -c] = FALSE
}
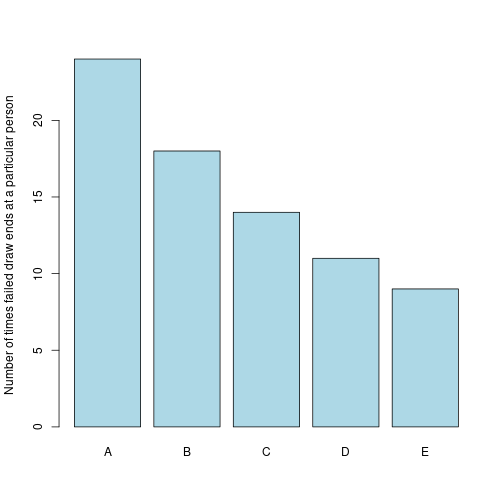
drawFails = rbind(singleFails,multiFails)

Out of 120 possible drawings, there are 76 failures.
So, if it fails, it is most likely to fail on the first draw. And the first failing draw is distributed as such:

colSums(drawFails)

##  A  B  C  D  E 
## 24 18 14 11  9

barplot(colSums(drawFails), ylab = "Number of times failed draw ends at a particular person",
        col = 'lightblue')