Predicting a runoff election

The riddle

As you may have seen in FiveThirtyEight’s reporting, there’s an election coming up. Inspired, Vikrant Kulkarni has an electoral enigma for you:

On Nov. 3, the residents of Riddler City will elect a mayor from among three candidates. The winner will be the candidate who receives an outright majority (i.e., more than 50 percent of the vote). But if no one achieves this outright majority, there will be a runoff election among the top two candidates.

If the voting shares of each candidate are uniformly distributed between 0 percent and 100 percent (subject to the constraint that they add up to 100 percent, of course), then what is the probability of a runoff?

Extra credit: Suppose there are N candidates instead of three. What is the probability of a runoff?

Functions and background

Here’s the plan:

1. Draw 3 numbers at random from the uniform distribution, \(x_1, x_2, x_3\) all on the interval \([0,1]\).
2. Convert these to vote fractions: \(f_i = \frac{x_i}{\sum_{i=1}^3 x_i}\).
3. Determine if there will be a runoff.

## This function will simulate the election and return TRUE if there is a need for a runoff.
simElection = function(nCandidates = 3){
    x = runif(nCandidates)
    f = x/sum(x)
    runoff = all(f<0.5)
    return(runoff)
}

1. Simulate a bunch and count the answer.

runoffProb = function(nSims, nCandidates=3){
    runoffCount = 0
    for(e in 1:nSims){
        runoffCount = runoffCount + ifelse(simElection(nCandidates=nCandidates),1,0)
    }
    prob = runoffCount/nSims
    return(prob)
}

Results

Let’s test this out for a few different numbers of simulated elections

simTests = round(10^(seq(from=2,to=6,by=0.5)),0)
set.seed(123) #For reproducibility
rProbs = sapply(simTests,FUN=runoffProb)
plot(simTests,rProbs, log='x',xlab = "Number of simulations", ylab= "runoff probability",
     ylim = c(0.3,0.7))
abline(h=0.5,col='blue',lty=3)
arrows(x0=simTests, y0=rProbs-sqrt(1/simTests), x1=simTests, y1=rProbs+sqrt(1/simTests), 
       code=3, angle=90, length=0.1)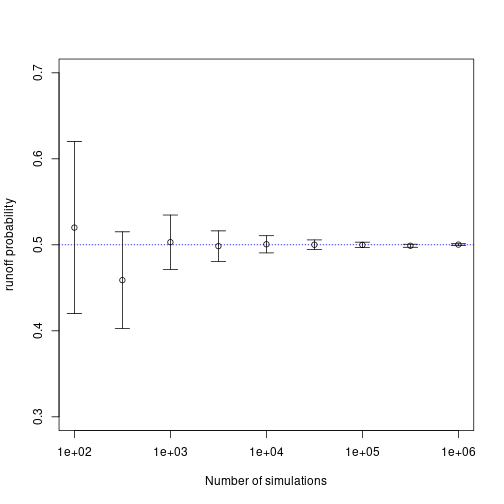

In this plot, the blue line indicates a runoff probability of 50%. Error bars are \(\sqrt{\frac{1}{N}}\) where \(N\) is the number of simulations run (and is likely an underestimate of the actual error).

The runoff probability for 10⁶ is 50.0235%, which rounds to 50% rather nicely. I’m certain that there is an analytic solution to this. I’m not going to hunt for it though.

EDIT: 10/19/2020: The preceding answer assumes that the number of voters is very large. The answer should depend on the number of voters. Consider these examples:

• 1 voter means there is never a runoff (regardless of the number of candidates).
• 2 voters require a runoff every time they disagree (and nobody wins when they disagree…ever), so the runoff probability is \(\frac{N-1}{N}\), where \(N\) is the number of candidates.

I fiddled around with some numbers (i.e., I will state it without proof), and I think that the runoff probability (for 3 candidates and \(N\) voters) is this: \(\frac{N+2}{2(N+1)}\) In the limit of large \(N\), this agrees with my result.

Extensions

Extra credit: Suppose there are N candidates instead of three. What is the probability of a runoff?

Since 10000 simulations was reasonably close to the correct simulated answer, let’s go up an order of magnitude and use that here. The blue line indicates 50% probability, the red line indicates 95% probability.

candidates = 2:10
set.seed(12345)
rProbsN = sapply(candidates,FUN=function(x){runoffProb(nSims = 100000,nCandidates=x)})
plot(candidates,rProbsN, xlab = 'Number of candidates', ylab = 'Runoff Probability',
     ylim = c(0,1))
abline(h=0.5,col='blue',lty=3)
abline(h=0.95,col='red',lty=2)
abline(v=5,col='red',lty=2)
arrows(x0=candidates, y0=rProbsN-sqrt(1/100000), x1=candidates, y1=rProbsN+sqrt(1/100000), 
       code=3, angle=90, length=0.1)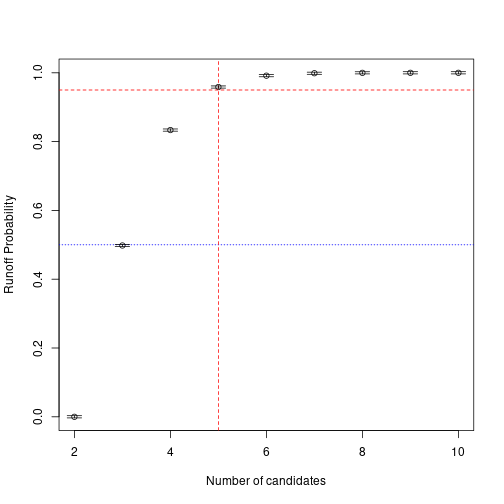

These are the values for the probabilities. The estimated error probability is on the order of \(10^{-3}\).

probTable = data.frame(candidates,rProbsN)
probTable

##   candidates rProbsN
## 1          2 0.00000
## 2          3 0.49799
## 3          4 0.83351
## 4          5 0.95867
## 5          6 0.99164
## 6          7 0.99873
## 7          8 0.99990
## 8          9 0.99999
## 9         10 1.00000

There aren’t any patterns that jump out at me (and to really differentiate between the higher number of candidates, I’d need more precision…so more sims and more computational time). For example 0.83351 seems really close to 5/6 = 0.8333333. But 0.95867 could be 22/23 or 23/24 (but probably not 24/25.) Short answer: when you get to 5 candidates, there is more than a 95% chance of a runoff.

Proposed related riddler question:

So, what seems more interesting to me is how changing the first-past-the-post rule (“Whoever gets the most votes wins”) to a majority rule (“You need 50% of the vote to win”) would allow a 3rd party to become more influential in a similar race. Right now, we generally have two parties, the red party and the blue party who rule in part due to the nature of this first past the post rule. So I would ask, “How popular does a 3rd party have to be to significantly impact the race by forcing a runoff more than 25% of the time on average?” It could explore these two cases:

• It is a hotly contested district/city/whatever and the majority parties evenly split the remaining probability. For example, it could be 45/45/10.
• There is a “one party rule” in the area. So the majority parties split the remining probability 60/40. For example, the probability split could be 54/36/10.