Guess the word
The riddle
Here is this week’s Riddler problem:
From Oliver Roeder, who knows a thing or two about riddles, comes a labyrinthine matter of lexicons:
One of Ollie’s favorite online games is Guess My Word. Each day, there is a secret word, and you try to guess it as efficiently as possible by typing in other words. After each guess, you are told whether the secret word is alphabetically before or after your guess. The game stops and congratulates you when you have guessed the secret word. For example, the secret word was recently “nuance,” which Ollie arrived at with the following series of nine guesses: naan, vacuum, rabbi, papa, oasis, nuclear, nix, noxious, nuance.
Each secret word is randomly chosen from a dictionary with exactly 267,751 entries. If you have this dictionary memorized, and play the game as efficiently as possible, how many guesses should you expect to make to guess the secret word?
Functions and background
Since the dictionary size is 267,751, let’s give that number a name. Let’s also create a function that gives the result of a word guess.
dictSize = 267751
dictionary = 1:dictSize
guessGame = function(guess, actual){
result = ifelse(guess == actual, 'win',
ifelse(guess < actual, 'after', 'before'))
return(result)
}For simplicity, I’m going to assume a “dictionary” of numbers. That way I don’t have to worry about pesky words.
I’m going to use a binary search algorithm. Basically, this algorithm picks the middle number in the sorted list and guesses that value. Best case: I guessed right and win. Worst case: I guessed wrong and reduced my possible choices by \(\geq\) 50%. (Why more than half? Well, consider this example where there are three choices left: 1, 2, or 3. The algorithm tells you to pick 2. This is incorrect, and the algorithm spits back “before” or “after”. This means that you now have 1 item to choose from out of the 3 that you started at. You’ve reduced the space by 2/3’s or slightly more than 66%. Obviously, this is a best case, but the same is true as the space gets bigger too.) Anyway, let’s make this function!
countBinarySearch = function(actual){
lowerBound=1
upperBound=dictSize
idx = 1
found = FALSE
while(!found){
if(upperBound<lowerBound){
stop('Upper bound is smaller than lower bound.')
}
## Build the dictionary
thisDict = lowerBound:upperBound
## Make a good guess
guess = lowerBound + (upperBound - lowerBound) %/% 2 # Integer division!
gameResult = guessGame(guess = guess, actual = actual)
if(gameResult == 'win'){
## Guess is correct, return the index
return(idx)
}else if(gameResult == 'before'){
## Value is smaller than guess.
upperBound = guess - 1
idx = idx + 1 # increment the index
}else if(gameResult == 'after'){
## Value is larger than guess.
lowerBound = guess + 1
idx = idx + 1 # increment the index
}else{
stop('Game result not possible.')
}
}
}Results
Before the crunching begins, let’s set some bounds. The best case is that the guessed value is the middle value that my algorithm guesses. So we should not get a result smaller than 1. The worst case is that I have to reduce the possibilities by half until I am left with only one choice. This is 19 choices.
Some would calculate the probability for each possibility, and while that seems tractable, I’m not going to do that. Let’s just count them all.
actualVals = dictionary
searchLength = vapply(actualVals, countBinarySearch, FUN.VALUE = numeric(1))
plot.ecdf(searchLength, ylab = 'cumulative probability', main='',
xlab = 'length of search')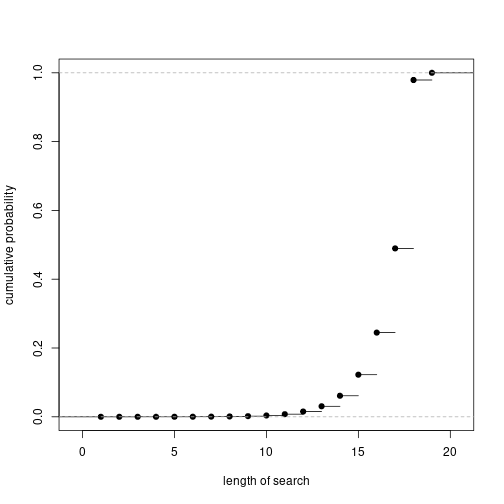
hist(searchLength, freq=FALSE, xlab = 'length of search')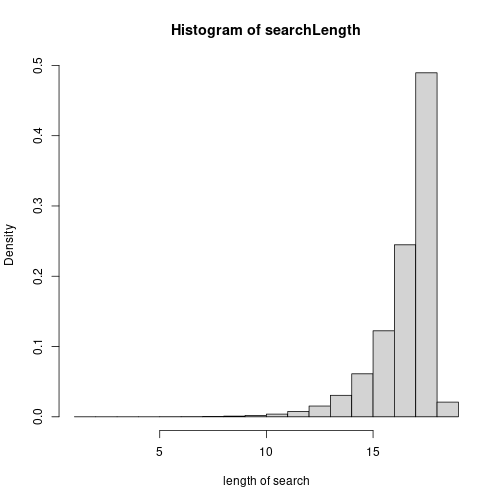
summary(searchLength)## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 1.00 17.00 18.00 17.04 18.00 19.00avgSearch = mean(searchLength)This means that we should expect to take 17.04 turns. The most common number of turns to take is 18. Table of results:
| searchLength | Freq |
|---|---|
| 1 | 1 |
| 2 | 2 |
| 3 | 4 |
| 4 | 8 |
| 5 | 16 |
| 6 | 32 |
| 7 | 64 |
| 8 | 128 |
| 9 | 256 |
| 10 | 512 |
| 11 | 1024 |
| 12 | 2048 |
| 13 | 4096 |
| 14 | 8192 |
| 15 | 16384 |
| 16 | 32768 |
| 17 | 65536 |
| 18 | 131072 |
| 19 | 5608 |
Extension
So this table hints at an elegant mathematical solution. It looks like the number of values for which it takes \(N\) guesses is:
\[2^{N-1}\]So the expectation value for this problem should be:
\[\langle g \rangle = \frac{\sum_{g=1}^{18} g 2^{g-1} + 19 \left(D - \sum_{g=1}^{18} 2^{g-1}\right)}{D}\]where \(D\) is the size of the dictionary. Let’s test this out:
g = 1:18
summation = sum(g*2^(g-1))
numerator = summation + 19 * (dictSize - sum(2^(g-1)))
g.expval = numerator/dictSizeAnd the expectation value from this calculation is 17.04 (rounded to two decimal places).