T-Shirt Cannon

The riddle

Riddler Puzzle

During a break at a music festival, the crew is launching T-shirts into the audience using a T-shirt cannon. And you’re in luck — your seat happens to be in the line of flight for one of the T-shirts! In other words, if the cannon is strong enough and the shirt is launched at the right angle, it will land in your arms.

The rows of seats in the audience are all on the same level (i.e., there is no incline), they are numbered 1, 2, 3, etc., and the T-shirts are being launched from directly in front of Row 1. Assume also that there is no air resistance (yes, I know, that’s a big assumption). You also happen to know quite a bit about the particular model of T-shirt cannon being used — with no air resistance, it can launch T-shirts to the very back of Row 100 in the audience, but no farther.

The crew member aiming in your direction is still figuring out the angle for the launch, which you figure will be a random angle between zero degrees (straight at the unfortunate person seated in Row 1) and 90 degrees (straight up). Which row should you be sitting in to maximize your chances of nabbing the T-shirt?

Functions and background

For this puzzle, we will utilize the range equation, which can be stated: \(R = \frac{v_i^2 \sin 2\theta_i}{g}\)

Here, \(\theta_i\) is the launch angle. Now, this is a useful equation if we have exact measurements for things like the muzzle velocity \((v_i)\), and the distance between the rows. Alas, we don’t have that. Instead, we have this statement: “…with no air resistance, it can launch T-shirts to the very back of Row 100 in the audience, but no farther.” We know that the maximum range happens when \(\theta_i = 45 \deg\). This implies that \(\sin 2\theta_i = 1\) for this angle, and we can write:

\[R_{\text{max}} = 100 \, \text{rows} = \frac{v_i^2}{g}\]

I always tell my students that we should use units that are convenient for the problem, so let’s use a distance unit of “rows”. (I’ll omit the distance units from my equation hereafter). So the range is:

\[R = 100 \sin 2\theta_i\]

Let’s make this a function. Note, I’ve discretized the result by using the floor function, and realizing that the first row is row 1.

projectileRange = function(theta){
  thetaRad = theta * pi/180
  pRange = 100*sin(2*thetaRad)
  pRange = floor(pRange) + 1
  pRange = ifelse(pRange>100,100,pRange)
  return(pRange)
}

Results

Let’s see where things land.

launchAngle = seq(from=0,to=90,by=0.01)
projectileRows = projectileRange(launchAngle)
maxRow = names(which(table(projectileRows)==max(table(projectileRows))))
row = data.frame('row'=projectileRows)
#hist(projectileRows,breaks=c(0,101),freq=TRUE)
ggplot(row, aes(x=row)) + geom_histogram(fill='blue', binwidth = 1)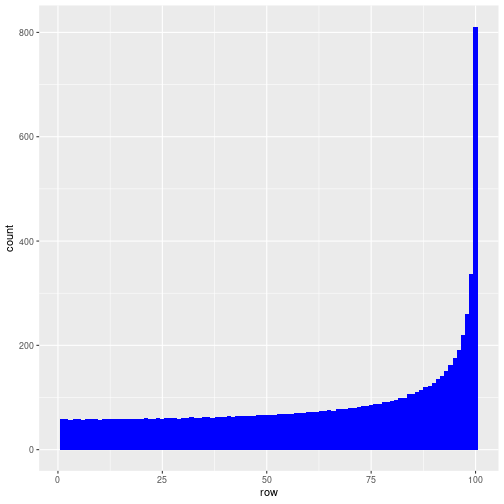

So the best row to sit in is row 100.

plot(launchAngle, projectileRows, col='blue', type='l', 
     xlab='Launch Angle (deg)', ylab = 'Row number')
minAngle = min(launchAngle[projectileRows==100])
maxAngle = max(launchAngle[projectileRows==100])
abline(v=minAngle, col='red', lty=3)
abline(v=maxAngle, col='red', lty=3)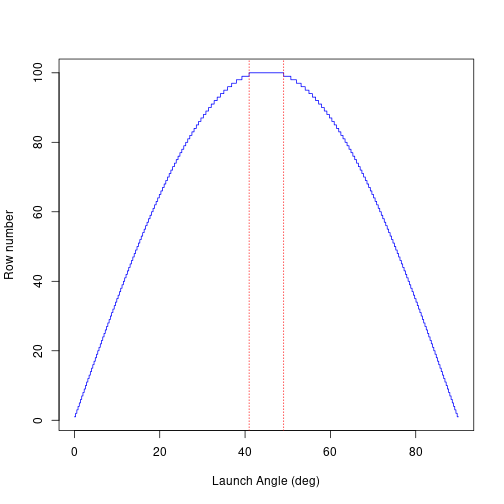

This may be counterintuitive. Looking at the figure below, it is easy to see what is going on. I’ve plotted the row the projectile lands in vs. the launch angle. The projectile row lands in row 100 between 40.95 deg and 49.05 deg. This is a range of 8.1 degrees. No other row has even half of that range of angles. It is the fact that the derivative of the range function is so small near an angle of 45 degrees, that makes the range change so little as the launch angle changes.