Making an unfair die

Turning a fair die into an unfair die

Here is this week’s Riddler problem.

You start with a fair 6-sided die and roll it six times, recording the results of each roll. You then write these numbers on the six faces of another, unlabeled fair die. For example, if your six rolls were 3, 5, 3, 6, 1 and 2, then your second die wouldn’t have a 4 on it; instead, it would have two 3s.

Next, you roll this second die six times. You take those six numbers and write them on the faces of yet another fair die, and you continue this process of generating a new die from the previous one.

Eventually, you’ll have a die with the same number on all six faces. What is the average number of rolls it will take to reach this state? Extra credit: Instead of a standard 6-sided die, suppose you have an N-sided die, whose sides are numbered from 1 to N. What is the average number of rolls it would take until all N sides show the same number?

Functions to build the simulation

There are two functions that I will use to accomplish the required tasks. First, we need to build the new die from the old die

makeNewDie = function(sides){
  newSides = sample(sides,replace=TRUE)
  return(newSides)
}

Then we will play the die game for a generic N sided die:

playDieGame = function(N){
  roll = 0
  dieSides = 1:N
  uniqueDieSides = unique(dieSides)
  while(length(uniqueDieSides)>1){
    # Roll the dice
    roll = roll + 1
    dieSides = makeNewDie(dieSides)
    uniqueDieSides = unique(dieSides)
  }
  return(roll)
}

Results for N=6

Let’s play the game 10000 times and find an average!

n = 10000
# Simulate the die game n times
gameResult = replicate(n, playDieGame(6))
avgResult = mean(gameResult)
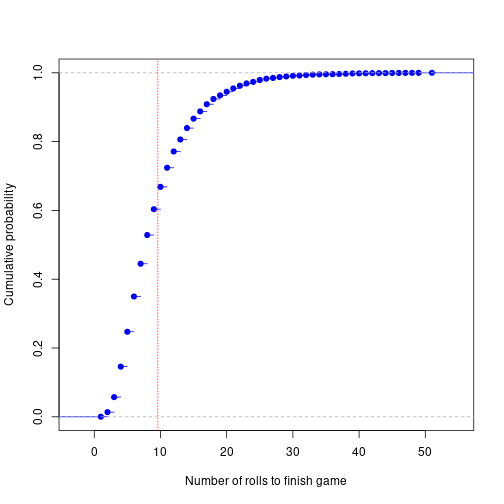
errResult = sd(gameResult)/sqrt(n)

The average number of rolls to end the game for a 6-sided die is: 9.611 ± 0.058.

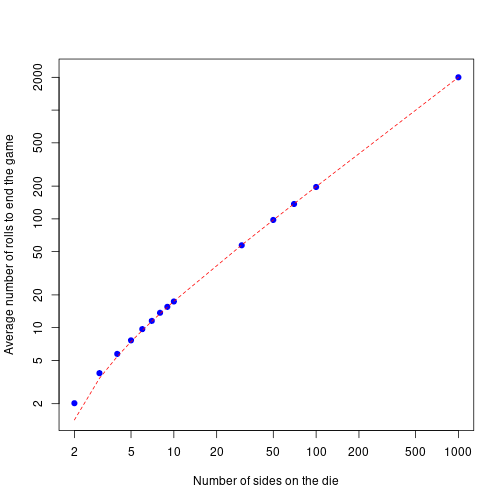
Results for more N values

Let’s check out some trends for different numbers of die sides to explore the trend. I will begin by doing a power law regression to see if the relationship is indeed linear.

nSims = 10000
dieSides = c(2:10,30,50,70,100,1000)
avgRes = NULL
seRes = NULL
for(nSides in dieSides){
  # Simulate the die game nSims times
  gameRes = replicate(nSims, playDieGame(nSides))
  avgRes = c(avgRes, mean(gameRes))
  seRes = c(seRes, sd(gameRes)/sqrt(nSims))
}
dieRoll.lm = lm(log10(avgRes) ~ log10(dieSides))
summary(dieRoll.lm)

## 
## Call:
## lm(formula = log10(avgRes) ~ log10(dieSides))
## 
## Residuals:
##       Min        1Q    Median        3Q       Max 
## -0.134117 -0.005829  0.021376  0.034802  0.041278 
## 
## Coefficients:
##                 Estimate Std. Error t value Pr(>|t|)    
## (Intercept)      0.11172    0.02832   3.945  0.00194 ** 
## log10(dieSides)  1.08924    0.02051  53.107 1.31e-15 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.05446 on 12 degrees of freedom
## Multiple R-squared:  0.9958,	Adjusted R-squared:  0.9954 
## F-statistic:  2820 on 1 and 12 DF,  p-value: 1.307e-15

It looks like the relationship between the average number of rolls and the number of sides on the die is linear. (Note that the slope of the previous regression is: 1.0892) Performing a linear regression, we see that there is a small offset.

dieRollLin.lm = lm(avgRes ~ dieSides)
summary(dieRollLin.lm)

## 
## Call:
## lm(formula = avgRes ~ dieSides)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -1.48426 -0.01724  0.15593  0.26103  0.60200 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -2.5892248  0.1560083   -16.6 1.22e-09 ***
## dieSides     2.0039608  0.0005784  3465.0  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.5478 on 12 degrees of freedom
## Multiple R-squared:      1,	Adjusted R-squared:      1 
## F-statistic: 1.201e+07 on 1 and 12 DF,  p-value: < 2.2e-16